Chap.II Machine Learning 機器學習

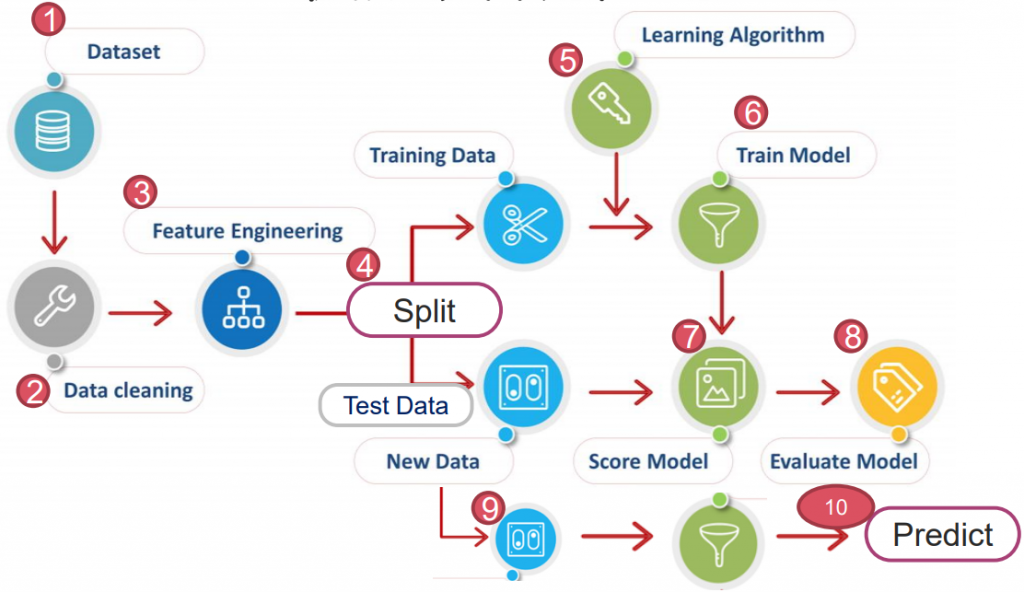
https://yourfreetemplates.com/free-machine-learning-diagram/

Part 1：Exploratory Data Analysis 資料探索與分析

Exploratory Data Analysis 又稱 EDA。
為瞭解資料的主要特性，會將蒐集而來的資料作分析，且常採用視覺化來進行判斷。
狹義來說，EDA 即資料收集/資料處理/視覺化...等過程。廣義來說，EDA 還包含 Data Clean。

1. Dataset（資料探索）：
2. Data Clean（資料清潔）：對資料進行一定程度的清潔，去除無項目項次、填滿或補 0 等。
   *一般機器學習過程中，資料探索與清潔是會交互處理的，會重複幾次甚至幾百次，直至獲取有意義的資料集。

1-1. Dataset 資料集

基本資料的匯入、找尋。純粹做練習用的資料如下：

1. UCI及其他套件（如：Scikit-Learn、Seaborn、StatsModels...等）
2. Kaggle　*世界最有名的資料競賽
3. Goole Dataset search
4. 政府部門資料

1-2. Data Clean 資料清潔

常包含以下幾個步驟：

1. Merge 合併資料
2. Rename 重新命名欄位名稱
3. Missing Value 遺失值
4. Transform column Data Type 資料類型轉換
5. Feature Engineering and Transforming Variables 特徵工程與變數轉換
6. Transform Numeric Variables 轉換數值變數
7. Remove Duplicate rows 移除重複值

1-3. Visualization 視覺化

常用的指令有幾種，包含 matplotlib(*補充看我、或我)、pandas 中的 plot 以及 seaborn(*補充看我)...等。

以下會以"tips"資料集來介紹 seaborn 的幾種圖：

# 載入必要套件 & 'tips' 資料集
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
tips = sns.load_dataset('tips')

1. 直方圖 sns.distplot：呈現單變數（也可用 histplot，但就沒有偏移曲線）

# 通常偏移分配，會多取 log 矯正
sns.distplot(np.log(tips['tip']), bins=20) # , kde=False

2. 關係散部圖 sns.relplot：用在 x y 關係為相對(另一絕對散部圖見補充 1.)

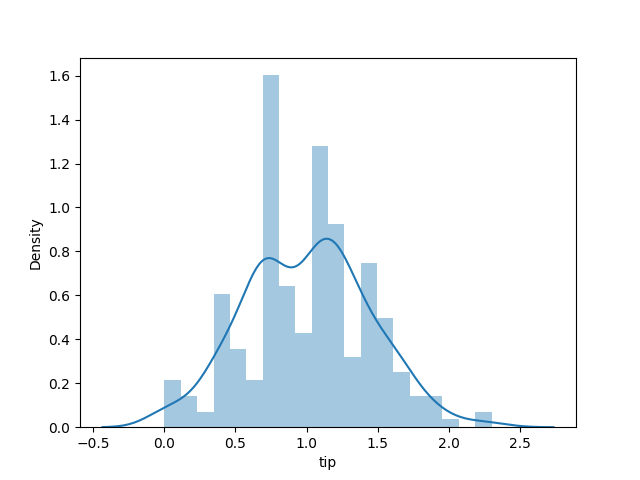
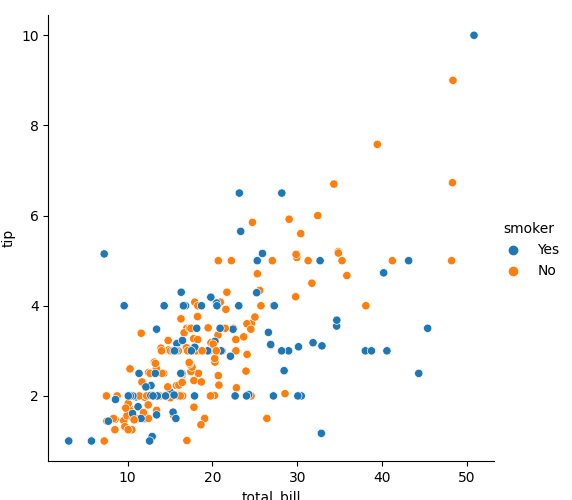
# hue= : 可以依照選擇 item 以顏色區分
sns.relplot(x='total_bill', y='tip', data=tips, hue='smoker')

3. 盒需圖 sns.boxplot

sns.boxplot(x='day', y='tip', data=tips, hue='sex')

4. 小提琴圖 sns.violinplot

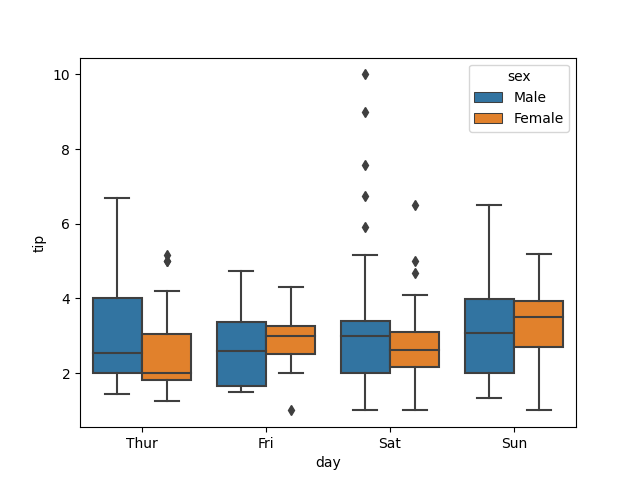
# split=True：可將 hue 的內容分布在兩側
sns.violinplot(x='day', y='tip', data=tips, hue='sex', split=True)

5. 點圖 sns.pointplot

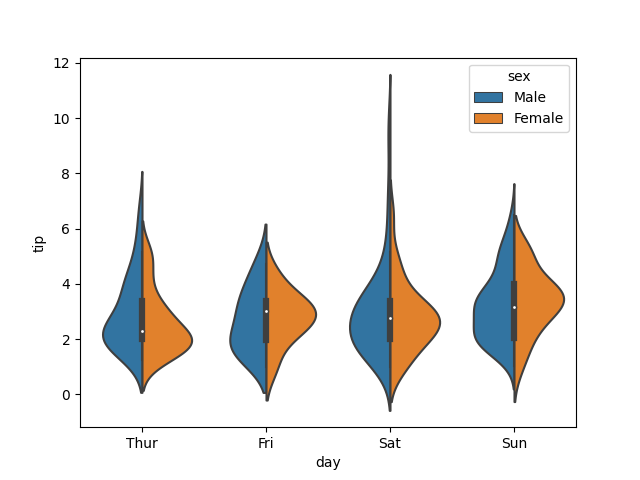
sns.pointplot(x='day', y='tip', data=tips, hue='sex')

6. 配對圖 sns.pairplot：把各個 item 配對成散部圖

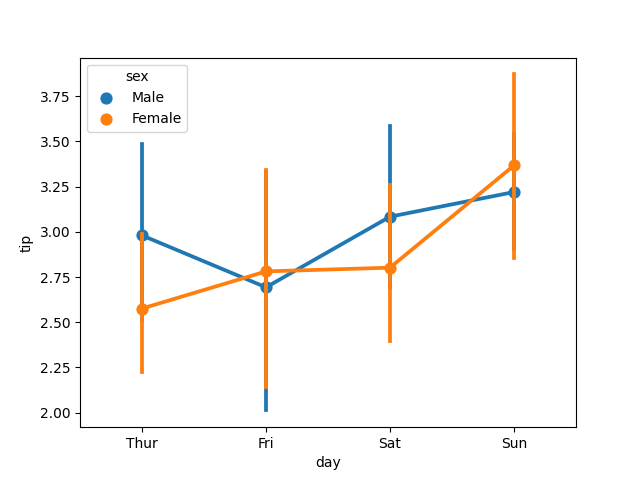
sns.pairplot(tips)

7. 熱力圖 sns.heatmap：把各個 item 配對，依照影響權重上色

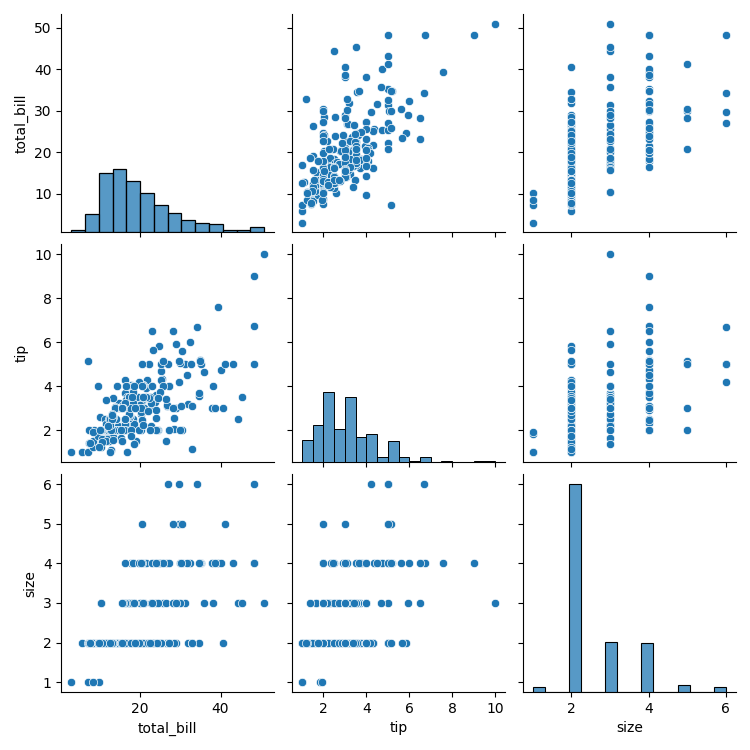
sns.heatmap(tips.corr())

看完以上，接著用經典範例-鐵達尼號 來操作 EDA：

1. Import tools & Load data

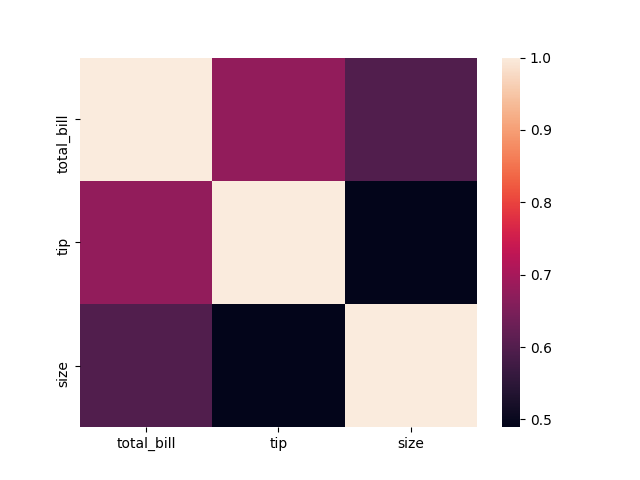
import pandas as pd
import seaborn as sns

df = sns.load_dataset('titanic')
df.head(10)

查看資料類型

df.info()

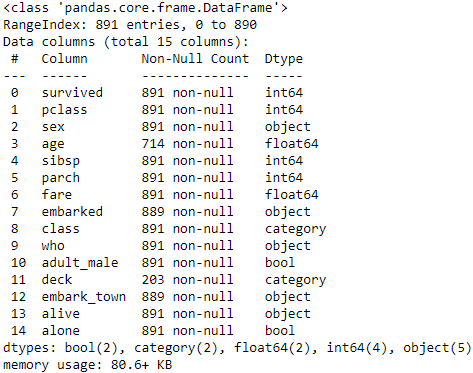
查看描述統計量

df.describe(include='all')

2. Analysis Y (此例中為'survived')

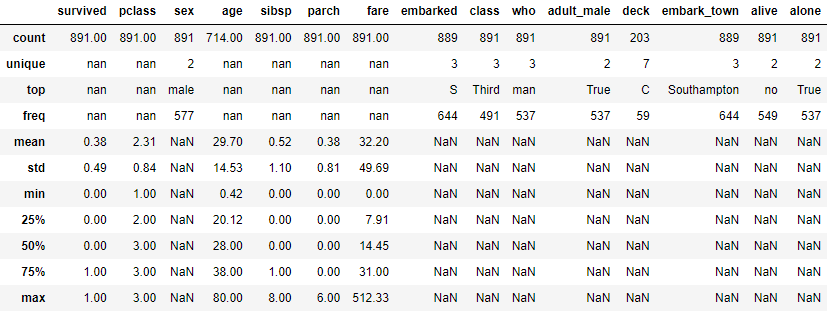
df['survived'].nunique()
>>  2

df['survived'].unique()
>>  array([0, 1], dtype=int64)

df['survived'].value_counts()
>>  0    549
    1    342
    Name: survived, dtype: int64

3. Deal w/ NaN value

# initial data
df.head()

# check NaN value
df.isna().sum()

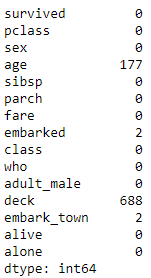
可以發現有許多重複/缺失項目，下面一項一項來處理：

A. 刪去重複項目

df.drop(['who', 'deck', 'embark_town','adult_male', 'deck', 'class', 'alive', 'alone'],
    axis=1, inplace=True)
df.head()

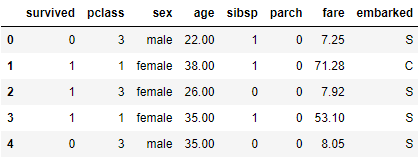
B. 填補缺失項目
B-1. 填補 age

df[df['age'].isna()]

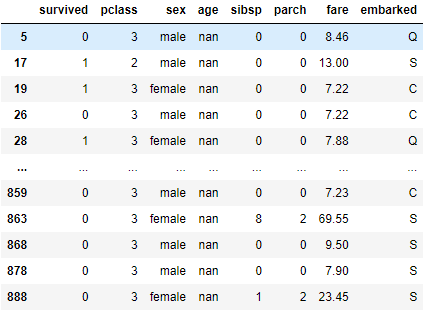
# 使用中位數來填補
df['age'].fillna(df['age'].median(), inplace=True)
df.iloc[[5, 17, 19, 26, 28]]   # 挑其中幾個檢查

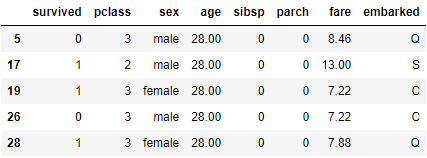
B-2. 填補 embarked

df[df['embarked'].isna()]

# 以前面一個的值填補
df['embarked'].fillna(method='ffill', inplace=True) # 或者 method='bfill'
df.iloc[[60, 61, 828, 829]]

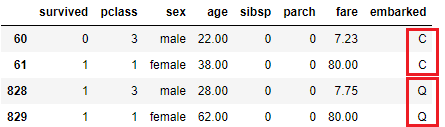
*Double check

df.isna().sum()

4. 轉換非數字資料

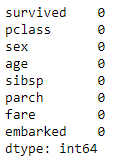
有序 ordinal: 特徵值隱含順序及大小高低之分 如: 'class' 'age' 等
名目 nominal: 不含順序大小 如: 'sex' 'embarked'
A. 將 'sex' 轉換為 0/1

df.sex.unique()
>>  array(['male', 'female'], dtype=object)

df.sex = df.sex.map({'male':1, 'female':0})
df.head()

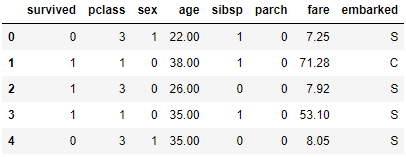
B. 將 'embarked' 轉換

# 確認登船港口 vs. 生存率
sns.barplot(data=df, x='embarked', y='survived')

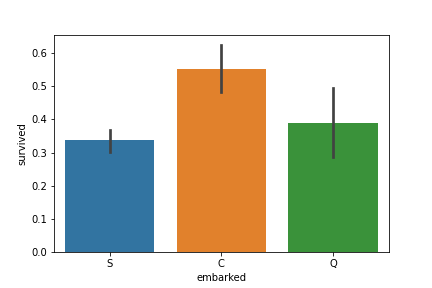
根據史料，登船港口依序為 Southampton -> Cherbourg -> Queenstown
此結果顯示登船港口與生存率無顯著相關，並沒有因為早上船而容易死亡。
故將其轉換為 one-hot encoding，避免影響判斷。

df.embarked.unique()
>>  array(['S', 'C', 'Q'], dtype=object)

# Transfer
df = pd.get_dummies(df, columns=['embarked'])
df.head()

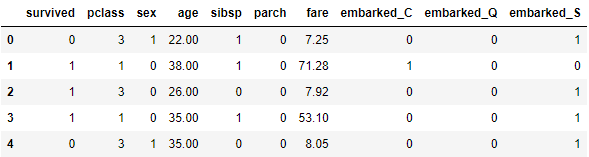
C. 將年齡轉換為級距
因考慮各個年齡層生存機率應相近，故使用 pd.cut() 將 'age' 切成幾個級距。
首先觀察各個級距存活率：

bins=[0, 12, 22, 30, 50, 60, 100]
age_cut = pd.cut(df['age'], bins)

sns.barplot(x=age_cut, y=df['survived'])

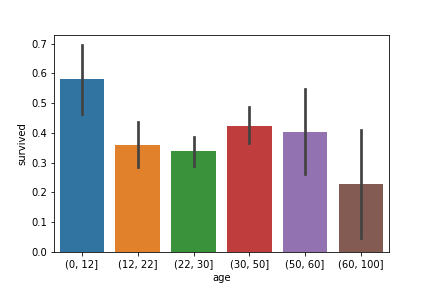
依據上圖，將各個年齡層進行有序 (ordinal) 編碼。生存機率最高為 5；最低為 0。

df['age'] = pd.cut(df['age'], bins, labels=[5, 2, 1, 4, 3, 0])
df.head()

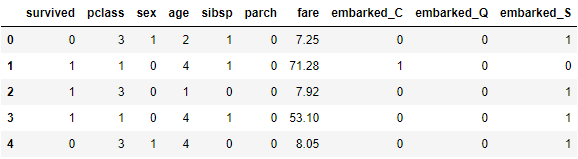
D. 歸一化 'fare'
找出票價為 0 者：

df[df['fare'] == 0]

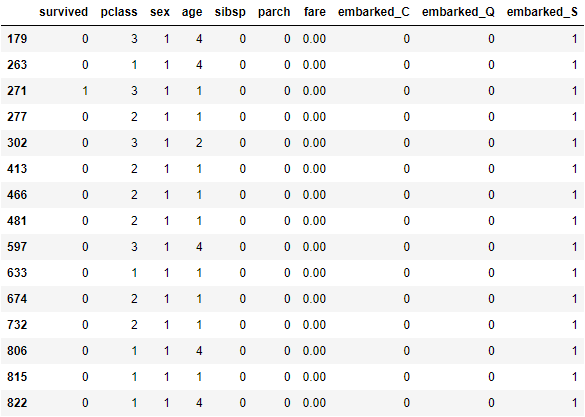
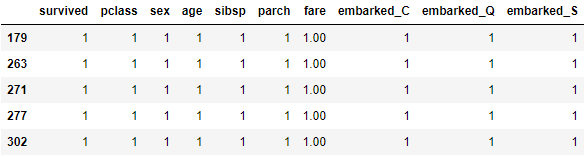
重設票價 0 為至少 1 塊錢：

df[df['fare'] == 0] = 1
df.iloc[[179,  263, 271, 277, 302]]

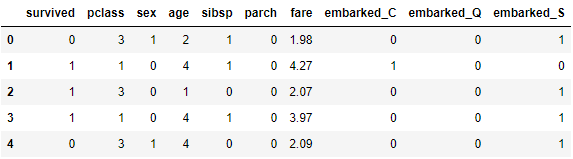
歸一化：

import numpy as np
df['fare'] = np.log(df['fare'])
df.head()

5. Analize relationship between X & Y

資料整理完成後 方可確認各個資訊間的關聯，以下用熱力圖做範例：

sns.set(style='ticks', color_codes=True)
plt.figure(figsize=(14, 12))
sns.heatmap(df.corr(), linewidths=0.1, square=True, linecolor='w', annot=True)
plt.show()

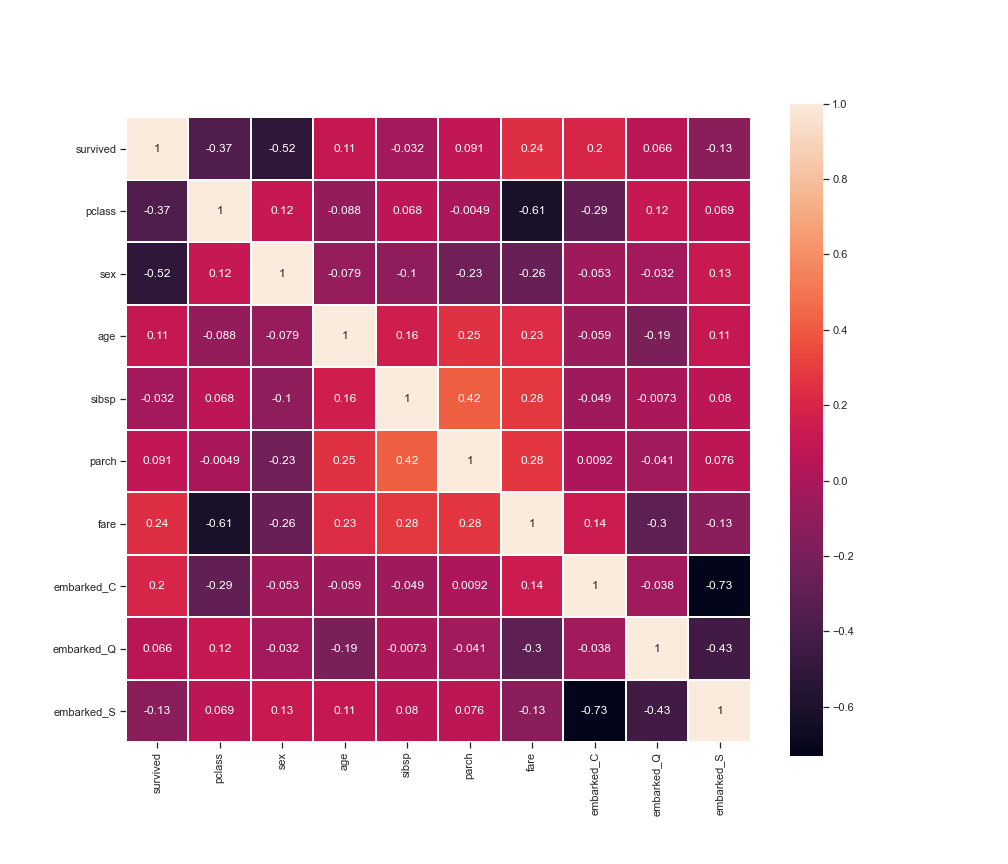
從以上分析可知：生存機率與艙等、性別高度相關。

6. Split Data

from sklearn.model_selection import train_test_split
y = df['survived']
X = df.drop('survived', axis=1)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

7. Feature Scaling (Normalization or Standardization)

為使收斂速度加快，通常在切割資料後會進行以下步驟其一：

1. 正規化 Normalization: 將資料等比例縮放到 [0, 1] 區間中。
   X_nor = (X - Min)/(Max-Min)
2. 標準化 Standardization: 將資料經 Z 轉成標準常態分佈 (Standard Normal Distribution)，即 X 距離 mean 有多少 std。
   X_std = (X - Mean)/(Sigma)

兩種方式皆可，在此處使用標準化：

from sklearn.preprocessing import StandardScaler
stdsc = StandardScaler()

X_train_std = stdsc.fit_transform(X_train)
X_test_std = stdsc.transform(X_test)

8. Modeling (Regression)

此處我們採用 LGBMClassifier 演算法

import lightgbm as lgb
from lightgbm import LGBMClassifier

clf = lgb.LGBMClassifier(
    objective = 'binary',
    learning_rate = 0.05,
    n_estimators = 100,
    random_state=0)

clf.fit(X_train_std, y_train)

9. Score Model

clf.score(X_test_std, y_test)
>>  0.8212290502793296

10. Evaluate Model

我們可以利用一些簡單的 AutoML，將所有演算法/參數跑一遍並評估可行性：

from lazypredict.Supervised import LazyRegressor, LazyClassifier

cls = LazyClassifier(ignore_warnings=False, custom_metric=None)
models, predictions = cls.fit(X_train_std, X_test_std, y_train, y_test)

11. Save & Load Model

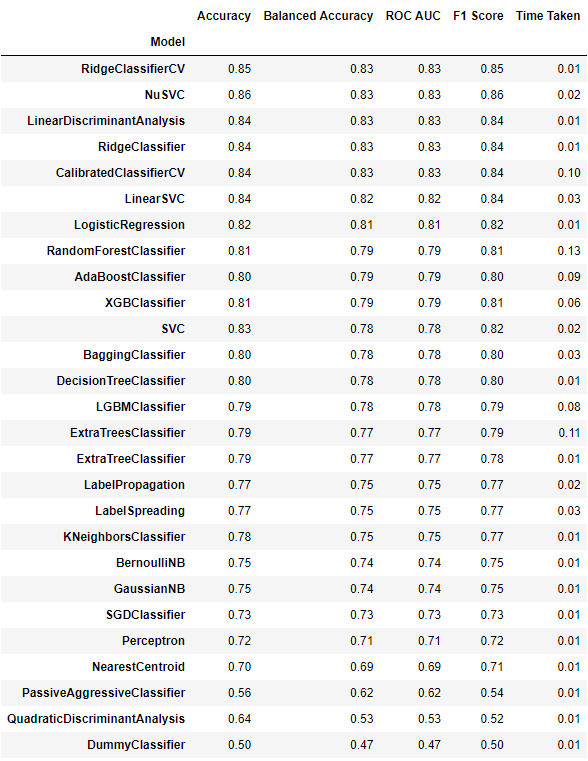
sklearn 有提供一內建存取方式

import joblib

model_file_name = 'model clf.joblib'
joblib.dump(clf, model_file_name)

讀取方式：

clf_load = joblib.load('model clf.joblib')

接著試著輸入資料來使用演算法
根據 EDA 的過程，會需要以下轉換函式

import pandas as pd
import numpy as np

def convent_sex(sex):
    return 1 if sex=='male' else 0


def convnet_age(age):
    bins=[0, 12, 22, 30, 50, 60, 100]
    return pd.cut([age], bins, labels=[5, 2, 1, 4, 3, 0])[0]

dict1 = {'C': 0, 'Q':1, 'S':2}
def convnet_embarked(embarked):
    x = dict1[embarked]
    if x == 0:
        return 1, 0, 0
    elif  x == 1:
        return 0, 1, 0
    elif  x == 2:
        return 0, 0, 1

Method 1. 用 list 輸入 (轉成 np array/DataFram)

X = []
X.append([2, convent_sex('male'), convnet_age(31), 1, 2, np.log(32), *convnet_embarked('Q')])
X.append([1, convent_sex('female'), convnet_age(28), 1, 2, np.log(500), *convnet_embarked('Q')])
X=np.array(X)

丟進演算法中

X_test = stdsc.transform(X)
y = clf_load.predict(X_test)

y
>>  array([0, 1], dtype=int64)

Method 2. 用 dict 輸入 (轉成 np array/DataFram)

X_1 = {
    'pclass':2,
    'sex': convent_sex('male'),
    'age': convnet_age(31),
    'sibsp': 1,
    'parch': 2,
    'fare': np.log(32),
    'embarked_C': 1, 'embarked_Q': 0, 'embarked_S': 0
    }
X_2 = {
    'pclass':3,
    'sex': convent_sex('female'),
    'age': convnet_age(28),
    'sibsp': 1,
    'parch': 2,
    'fare': np.log(500),
    'embarked_C': 1, 'embarked_Q': 0, 'embarked_S': 0
    }

df = pd.DataFrame([X_1, X_2], index=[0, 1])
df

丟進演算法中

X_test = stdsc.transform(df)
y = clf_load.predict(X_test)

y
>>  array([0, 1], dtype=int64)

至此，就完成了經典題目：鐵達尼號 的演算法演練了！

結論：

EDA 為在資料收集完成後的前處理，相對其他步驟來說，是最重要的步驟。
若資料處理（補償、合併、刪除）不夠全面，將導致演算法 output 出一個不夠全面的模型，使預測失準。
.
.
.
.
.
*補充1.：
絕對散部圖 sns.catplot：用在 x y 關係為絕對

sns.catplot(x='day', y='tip', data=tips, hue='sex')

.
.
.
.
.

Homework Ans：

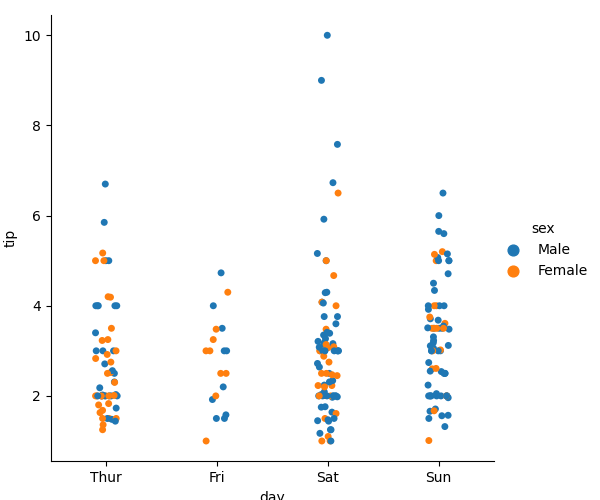
使用假設檢定，檢定近40年(10屆)美國總統的身高是否有差異?
(Data: president_height.csv)

1. Data Set

import pandas as pd
df = pd.read_csv('./president_heights.csv')
height = df['height(cm)']

2. 建立雙樣本：A. 近10屆 (Sample2) B. 其他總統 (Sample1)

from scipy import stats
sample1 = height.head(len(df)-10)
sample2 = height.tail(10)

3. ttest 檢定 (兩樣本獨立)

z, p = stats.ttest_ind(sample1, sample2)
print(f'Z-value: {z}')
>>  Z-value: -2.69562113651512
print(f'P-value: {p}')
>>  P-value: 0.010226470347307223

4. 作圖 (直方圖)

# 根據 sample1 平均值 & 樣本標準差，劃出抽取 100000 次分配
s1_bar = np.random.normal(sample1.mean(), sample1.std(), 100000)
plt.hist(s1_bar, bins=100)
plt.axvline(s1_bar.mean(), c='y', linestyle='--', linewidth=2)

# 計算信心水準 95%，雙尾檢定結果(一邊 2.5%)的 x_bar 值
ci = stats.norm.interval(0.95, s1_bar.mean(), s1_bar.std())
plt.axvline(ci[0], c='r', linestyle='--', linewidth=2)
plt.axvline(ci[1], c='r', linestyle='--', linewidth=2)

# 根據 mean + t*s 劃出對立假設 x_bar 落點
plt.axvline(s1_bar.mean() + z*s1_bar.std(), c='m', linestyle='--', linewidth=2)
plt.savefig('pic HW9-2')
plt.show()

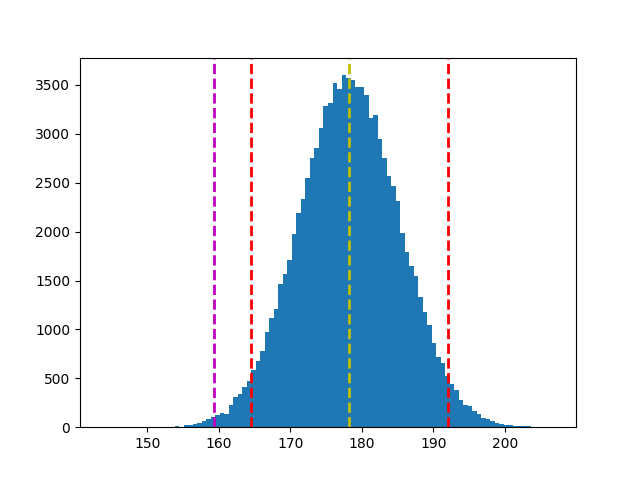
結論：近40年(10屆)美國總統的身高有顯著異於前任總統。
.
.
.
.
.

Homework：

請參考鐵達尼號的流程，使用鑽石清理資料來完成演算法。